Köhler theory

Köhler theory describes the process in which water vapor condenses and forms liquid cloud drops, and is based on equilibrium thermodynamics. It combines the Kelvin effect, which describes the change in saturation vapor pressure due to a curved surface, and Raoult's Law, which relates the saturation vapor pressure to the solute.^[1] It is an important process in the field of cloud physics.

Köhler equation:

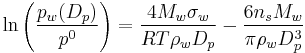
$\ln \left ( \frac{p_{w}(D_{p})}{p^{0}} \right ) = \frac{4M_{w}\sigma_{w}}{RT\rho_{w}D_{p}} - \frac{6n_{s}M_{w}}{\pi\rho_{w}D_{p}^{3}}$

where 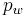$p_w$ is the droplet water vapor pressure, 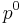$p^0$ is the corresponding saturation vapor pressure over a flat surface, 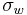$\sigma_w$ is the droplet surface tension, 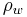$\rho_w$ is the density of pure water, 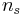$n_s$ is the moles of solute, 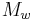$M_w$ is the molecular weight of water, and 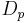$D_p$ is the cloud drop diameter.

Köhler curve

The Köhler curve is the visual representation of the Köhler equation. It shows the supersaturation at which the cloud drop is in equilibrium with the environment over a range of droplet diameters. The exact shape of the curve is dependent upon the amount and composition of the solute. The Köhler curves where the solute is sodium chloride are different than when the solute is sodium nitrate or ammonium sulfate.

The figure above shows three Köhler curves of sodium chloride. Consider a point on the graph where the wet diameter is 0.1 micrometers and the supersaturation is 0.35%. Since the relative humidity is above 100%, the droplet will grow until it is in thermodynamic equilibrium. As the droplet grows, it never encounters equilibrium, and thus grows without bound. However, if the supersaturation is only 0.3%, the drop will only grow until about 0.5 micrometers. The supersaturation at which the drop will grow without bound is called the critical supersaturation. The diameter at which the curve peaks is called the critical diameter.

References

^ "Köhler Theory 101". http://www.chbe.gatech.edu/fac_staff/faculty/nenes/kta/KTA%5B1%5D_files/page0001.htm. Retrieved 2008-10-23.

Rogers, R. R., M. K. Yau, 1989. A Short Course in Cloud Physics, 3rd Ed. Pergamon Press. 293 pp.
Young, K. C., 1993. Microphysical Processes in Clouds. Oxford Press. 427 pp.
Wallace, J. M., P.V. Hobbs, 1977. Atmospheric Science: An Introductory Survey. Academic Press. 467 pp.